
去年年底,俺好友「Dr. 史考特。哈蘇」(見上圖) 從密爾瓦基打電話給我,問我有沒有「狗屎」...啊不對,是「Gauss」啦~
我跟他講這套軟體基本上從俺離開清大統研所後就再也沒有見到有人在用了。
我剛進清大統研時,看到一堆學長姐在用這套軟體跑模擬。
可是 debug 過程相當麻煩,所以我就沒有去研究了。
事實上,到了我們這一屆開始寫論文時,整所也只剩下我麻吉「賴桑」用 Gauss 跑模擬。
我們曾經趁著統研盃時問了一下其他統研所的學生,好像大家還是比較常用 S+,似乎 Gauss 變成清大統研專用的模擬軟體似的。
無論如何,我知道我朋友常用 SAS 和 Stata,怎麼這回突然要用 Gauss?
結果他說他投稿了一篇paper,裡面用 probit model 分析資料,但 reviewer 傳回來的意見是:你怎麼沒做 normal assumption test 啊?
後來他一查,發現 probit model 底下的 normal assumption test 需要使用「Bera-Jarque-Lee test」進行檢定。
問題來了,他翻遍了 SAS 和 Stata 的手冊,都沒有發現裡面有內建這個檢定的語法。
可是 Gauss 有內建,所以他想要搞來這套軟體完成這個 reviewer 的要求。
我本來是覺得怎麼可能,Stata 我是完全不懂,但 SAS 好歹會有吧?!
結果自己翻遍了SAS手冊,還真的是沒有......
重點是,我沒有 Gauss 可以借他~
另外,我也根本不曉得這個 Bera-Jarque-Lee test 長什麼模樣。
當時懶得去 google,而剛好史考特先生手邊有一篇專門在講這個檢定的 paper,所以他就傳一份給我。
A simple representation of the Bera–Jarque–Lee test for probit models
我花了幾分鐘掃瞄了一下,發現這篇並不是這個檢定的第一篇 paper,而是把原來的檢定程序簡化,免除了一切複雜的矩陣運算。
所以我先稍微介紹一下這個檢定的流程:
假設一個 probit model 如下所示:

其中殘差 Ui 的密度函數 f(Ui) 經過偏微之後變成:
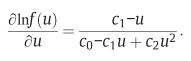
其中,c0 =σ^2,而 c1 和 c2 分別是 skewness 和 kurtosis。
因此,若 Ui 要是常態分配的話,c1 和 c2 最好都是 0 。
所以這段假設檢定可以設成:
H0: c1=c2=0 v.s. H1:c1或c2任一不為0
OK,接下來就不講原來 Bera-Jarque-Lee test 的公式,直接來看 Dr. Wilde 這篇 paper 是教我們如何簡化整個檢定的過程。
有別於其他檢定大都是直接拿一些參數來算,簡化版的 Bera-Jarque-Lee test 需要去配適這個線性迴歸:
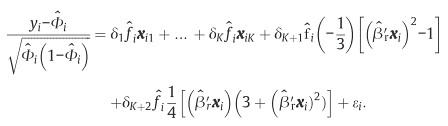
裡面的 yi, xi都是原始資料,等號左邊的 Φi_hat 是 β_hat'*x 的 cdf,這個 β_hat' 就是原先 probit model 裡面的所有估計參數所排成的向量。
等號右邊裡面,δ1~δk+2 是我們需要跑程式去估計的參數,而
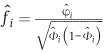
其中,ψi_hat 是 β_hat'*x 的 pdf。
估計出 δ1~δk+2 之後,就可以算出每個觀測值的預測值,接著再算出每個預測值平方和,再拿來跟卡方分配(df=2)去比較,其 p-value 若大於 0.05 就表示不拒絕虛無假設,則這個 probit model 就沒有違背 normal assumption。
而上述流程其實自己用 SAS 就可以寫的出來,後來我告訴史考特先生怎樣寫,他寫完後我再debug看沒有問題後,就成功完成了這項任務。
在這邊分享一下 SAS 程式碼:
步驟一:先配適 probit model。
proc sort data=chien.admit;
by descending admit;
run;
proc probit data=chien.admit order=data;
class admit;
model admit= gre gpa topnotch;
output out=chien.out xbeta=xbeta;
run;
此處唯一要注意的是,必須把 xbeta 這個數據全部另存新檔(chien.out),因為這個新檔裡面就是包含著 β_hat'*x 的數據。
步驟二:利用新檔計算上面列出的那個線性迴歸模式裡面的一些物件。
data chien.out;
set chien.out;
pxbeta=pdf('NORMAL', xbeta,0,1);
cxbeta=cdf('NORMAL', xbeta,0,1);
DV=(admit-cxbeta)/sqrt(cxbeta*(1-cxbeta));
fi=pxbeta/sqrt(cxbeta*(1-cxbeta));
IV1=gre*fi;
IV2=gpa*fi;
IV3=topnotch*fi;
A=(-(xbeta*xbeta-1)/3)*fi;
B=((xbeta*(3+xbeta*xbeta))/4)*fi;
run;
其中,
pxbeta = β_hat'*x 的 pdf。
cxbeta = β_hat'*x 的 cdf。
DV 就是計算線性迴歸等號左邊的 dependent variable。
fi 就是↓↓↓↓↓↓↓↓↓
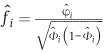
IV1, IV2, IV3, A 和 B 就是計算線性迴歸等號右邊的所有 independent variables。
步驟三:把步驟二算出來的 DV 和 IVs 拿去配適線性迴歸。
proc reg data=chien.out;
model DV = IV1 IV2 IV3 A B /noint;
output out=chien.LM p=predict;
run;
重點在於必須使用 output statement 把所有預測值另存新檔(chien.LM)。
步驟四:計算預測值的平方和:
data chien.LM;
set chien.LM;
predict2=predict*predict;
run;
proc means data=chien.LM sum;
var predict2;
run;
步驟五:計算 p-value。
proc iml;
chisq=XXX;
pchisq=1-probchi(chisq,2);
print pchisq;
run;
其中 XXX 請填入上面 proc means 的輸出結果。
大致的作法至此告一段落,我準備寫一個比較 general 的 macro 投稿去 SAS Global Forum,不過還有一些困難需要解決,所以就先不分享這個 macro 了。



 留言列表
留言列表
